Semantics of the liar paradox   Semántica de la paradoja del mentiroso   C. P. Hertogh Free University Brussels –(VUB-BE/EU) noromyxo2005@gmail.com https://orcid.org/0000-0002-6778-4837   DOI https://doi.org/10.48204/2805-1815.8475
INFORMACIÓN DEL ARTÍCULO	ABSTRACT/RESUMEN
Recibido el:12/1/2025 Aceptado el: 22/8/2025   Keywords: Excluded middle, non-contradiction, paraconsistent logic, semantics,  truth   Palabras clave: Medio excluido, no contradicción, lógica paraconsistente, semántica, verdad	Abstract: Although Liar-type conundrums –traditionally considered sophistry– do not match all characteristics of thought experiments (TE), particularly not the pragmaticist condition that thought experiments are designed to resolve predefined problems, we apply TE analyses and interpretations. The Liar (or, let's say, Liar-type statements involving truth (predicates), self-reference as in the fields of conceptual analysis, semantics and set theory) rose to paradigmatic, revolutionary prominence by Tarski's Gödelian logicistic deliberations in the beginning of last century now considered the orthodox semantic account. We survey semiotic and pragmatic accounts from the second half of last century and (non)classical (meta)logical accounts  that may gain traction in 21st century. Our resolution is manifold, both semantic and pragmatic. We show that modern logic, from the very beginning in Wittgenstein, has had more than two truth-values, next to T(rue) and F(alse), 'nonsense', 'meaningless', 'senseless', etc. We show that the Liar may bring up for discussion logical principles like law of excluded middle (LEM) and noncontradiction (LNC) and refute strong versions of these logical laws. We propose a pragmatic Gricean account of the Liar, analyzing Epimenides's and Eubulides' versions of the Liar as falsification of generic tacit conversational principle –Grice’s maxim of quality and maxim of manner– that people usually speak truthful, speak perspicuously. By application of TE Matrix Epimenides-style and Eubulides-style paradoxes can be extended to valid and sound modus tollens-style arguments with logical force of enthymeme. Resumen: Aunque los enigmas como la paradoja del mentiroso —tradicionalmente considerados sofistería— no se ajustan a todas las características de los experimentos mentales (TE), en particular a la condición pragmaticista de que los experimentos mentales están diseñados para resolver problemas predefinidos, aplicamos análisis e interpretaciones de TE. La paradoja del mentiroso (o, digamos, las afirmaciones de tipo mentiroso que involucran, verdad (predicados), autorreferencia, como en los campos del análisis conceptual, la semántica y la teoría de conjuntos) alcanzó una prominencia paradigmática y revolucionaria gracias a las deliberaciones logicistas gödelianas de Tarski a principios del siglo pasado, ahora consideradas la explicación semántica ortodoxa. Examinamos las explicaciones semióticas y pragmáticas de la segunda mitad del siglo pasado y las explicaciones (meta)lógicas (no)clásicas que podrían cobrar fuerza en el siglo XXI. Nuestra resolución es múltiple, tanto semántica como pragmática. Demostramos que la lógica moderna, desde sus inicios, Wittgenstein ha tenido más de dos valores de verdad, además de Verdadero y Falso, 'sinsentido', etc. Mostramos que la paradoja del mentiroso puede llevar a replantear principios lógicos como la ley del tercero excluido (LEM) y la no contradicción (LNC), y refutamos versiones fuertes de estas leyes lógicas. Proponemos una explicación pragmática griceana de la paradoja del mentiroso, analizando las versiones de Epiménides y Eubulides como una falsificación del principio conversacional tácito genérico —la máxima de calidad y la máxima de modo de Grice— según el cual las personas suelen hablar con la verdad y con perspicacia. Mediante la aplicación de la Matriz TE, las paradojas de Epiménides y Eubulides pueden extenderse a argumentos de estilo modus tollens válidos y sólidos con la fuerza lógica del entimema.

 

Identifications

The Liar appears in different versions throughout history of logic and philosophy (for recent discussions, see Martin, 1974, 1984; Beall et al. 2016/2023). We will particularly focus on semantic (instead of set theoretical) versions, such as Epimenides (7th-6th cent. BCE) and Eubulides (4th cent. BCE) versions.

Epimenides-type Liar paradoxes,

The Cretan says, 'All Cretans are liars'.                                                             [a]

The paradox is also in the Bible, New Testament, Titus I, 12 (Kripke, 1975, p. 690),  NABR (New American Bible (Revised Edition)):

“One of them, a prophet of their own, once said, 'Cretans have                                   [b]

always been liars,  vicious beasts, and lazy gluttons'”.

From point of view of present-day Critical Thinking courses, it appears to be a strongly emotional utterance of a negative prejudice against Cretan people, which bias should be removed, after which the proposition may have lost most of its cognitive content, too. It is one more reason not to allow for full range application of universal quantifier, since it seems to be an emotional exaggeration and for that reason already only partly true or not true at all.

Nevertheless, we will discuss and analyse this version in a foremost logical way as the logical paradox it has been turned into by history of logic and philosophy.

Eubulides-type Liar paradoxes,

A man says: “What I am saying now is a lie”.                                                    [c]       

This statement is false.                                                                                         [d]

The Liar or pseudomenos (ψευδόμενος) paradox is well-known in logic as a false, sophistical species of syllogism. Eubulides is also mentioned as conceiver of some more sophistic paradoxes, such as The Heap and The Bald Man. Traditionally, and postmodernistically again, these paradoxes are discussed in logic and linguistics as about vague or ambiguous predicates.

For the mathematical modern set theoretic versions (as Russell's Paradox, semantic version called The Barber) that aim at developing axiomatized logical systems, a more formal and abstract account may be required, which may be applied in development of computer languages, computer science, AI (Artificial Intelligence), IT (Information Technology).

We will survey some semantic historical accounts and then propose a semantic, pragmatic account touching here and there on insights from formal logical analyses of natural language, applying Chomsky linguistics (Chomsky, 1957/2002) and Kripke semantics (Kripke, 1975, 1980, 1982, 2019),

Fourfold Definition

We propose a four-fold definition of TE

1.        Ontologically speaking, TE are mental phenomena.

2.         After linguistic and hermeneutic turn, TE are TE texts

3.        Logically speaking, TE are incomplete arguments (enthymemes).

4.        On pragmaticist view, TE are mental devices designed to resolve predefined problems (analogous to experiments in science). (See also, Hertogh, 2015, 2018, 2023a on Galileo, 1638/1914; Hertogh, 2024 on Einstein & Infeld, 1938).

Traditionally considered sophistry the Liar does not live up to the fourth condition, since the Liar-type statements were not designed to resolve predefined problems, but rather to show limits of logic.

Also, they miss TE-indicators as 'Consider …', 'Imagine …', etc. Nevertheless, we may try and apply TE analyses and interpretations.

Crucial Thought Experiments

The Liar rose to logical prominence with Tarski's Gödelian (1933/1935) account. Tarski considers the Liar crucial experiments, which should be crucial thought experiments, since it is not about empirical sciences but mathematics and logic, which experiments don't need confirmation by execution in external reality since the basic entities of mathematics and logic only exist in the mind as ideal entities or nowadays in virtual space (as line, circle, numbers), which can only be physically approximated on Planet Earth.

Personally, as a logician, I could not reconcile myself with antinomies as a permanent element of our system of knowledge. However, I am not the least inclined to treat antinomies lightly. The appearance of an antinomy is for me a symptom of disease. Starting with premises that seem intuitively obvious, using forms of reasoning that seem intuitively certain, an antinomy leads us to nonsense, a contradiction. Whenever this happens, we have to submit our ways of thinking to a thorough revision, to reject some premises in which we believed or to improve some forms of argument which we used. We do this with the hope not only that the old antinomy will be disposed of but also that no new one will appear. To this end we test our reformed system of thinking by all available means, and, first of all, we try to reconstruct the old antinomy in the new setting; this testing is a very important activity in the realm of speculative thought, akin to carrying out crucial experiments in empirical science. (Tarski,1969, pp. 4-5)

Possibly the Liar could be considered kind of consistency TE test.

Mathematical Thought Experiments

Updated modern versions of the Liar may be considered paradigmatic or revolutionary thought experiments, as arising in 'foundational crises' contributing to theory change, a 'new conceptual framework'.

In Horowitz's & Massey's (1991) pivotal collection of essays on thought experiments in philosophy and science, Dionysios Anapolitanos contributes an essay on thought experimentation and conceivability conditions in mathematics, in which set theoretical paradoxes are discussed both as incentives to TE and TE themselves,

The third group includes thought experiments in mathematics performed fervently during and immediately after a foundational crisis. The overall activity during such periods is mainly centered around the construction of a new conceptual framework wherein the source of crisis in the old framework is hoped to be tamed… The best and the most well-known example of such creative activity spurred by a foundational crisis is the one occurred at the beginning of the 20th century during and after the appearance of the set-theoretic paradoxes. Various proposals concerning the modification of the naive Cantorian concept of set were put forwards with some notable among them those of the Russellian theory of types, of the Zermelo-Fraenkel theory of sets and of the Gödel-Bernays set theory… All these proposals not only started as thought experiments, but they were thought experiments in the sense of open-ended explanatory attempts in a playful and in a state of crisis conceptual framework, which, so to speak, was set free in motion by the emergence of the paradoxes. (Anapolitanos, 1991, p. 93)

An example of a set theoretic paradox in mathematical logic is so-called Russell's Paradox, which comes together with popular version of Barber Paradox, which is akin to Epimenides's version of the Liar asking  'whether a class is a member of itself or not', which may yield a contradiction “... the question whether the barber shaves himself or not. You can define the barber as 'one who shaves all those, and those only, who do not shave themselves.' The question is, does the barber shave himself?” (Russell, 1919 , pp. 354-355)¹, which argument Russell concludes to 'nonsense'

... But in our previous form I think it is clear that you can only get around it by observing that the whole question whether a class is or is not a member of itself is nonsense, i. e., that no class either is or is not a member of itself, and that it is not even true to say that, because the whole form of words is just a noise without meaning. (Russell,1919, p. 355)

Wittgenstein proposed a resolution in Tractatus 3.333, referring to the functions variant rather than the classes variant of the paradox, arguing a function cannot be an argument of itself nor contain itself, possibly demonstrating it as by adding existential quantification (∃ϕ) over argument (u): “This is at once clear, if instead of ‘F(F(u))’ we write ‘(∃ϕ): F(ϕu) . ϕu = Fu’. Herewith Russell’s paradox vanishes”, (Wittgenstein, 2022, #3.333) which formulas, however, may appear equivocal on interpretation, even involving discussions on a possible misprint in some editions of Tractatus (see Black, 1964; Jolley, 2004; Sutrop, 2009).  We will come back to it in section about senselessness (Beyond Two Truth Values).

Paradigmatic Thought Experiments

The terms paradigmatic or revolutionary TE are derived from Kuhn's The Structure of Scientific Revolutions. Focusing on TE in physics, Kuhn holds that paradigmatic TE contribute to theory change in times of foundational crisis:

It is no accident that the emergence of Newtonian physics in the seventeenth century and of relativity and quantum mechanics in the twentieth century should have been both preceded by and accompanied by fundamental philosophical analyses of the contemporary research tradition. Nor is it an accident that in both these periods the so-called thought experiment should have played so critical a role in the progress of research. As I have shown elsewhere, the analytical thought experimentation that bulks so large in the writings of Galileo, Einstein, Bohr, and others is perfectly calculated to expose the old paradigm to existing knowledge in the ways that isolate the root of the crisis with a clarity unattainable in the laboratory. (Kuhn, 1970, p, 88)

 

Paradoxes

We may define paradoxes like this: Paradoxes are defined in this paper as metalogical instruments that question their very presuppositions or the presuppositions of the (logical) system they are part of.

Like TE they may be resolved by Extended Argument analyses, i.e., by explicitation of rules, principles, presuppositions that validate them as (logical) arguments, within a different or more encompassing (logical) system.

They are enthymemes in senso stricto when it is about finding a major under which they may subsume as minor. The missing premises, presupposition, etc., that make them come true, may be found in immediate context or theory (immanent or internal analyses), or outside immediate context or theory (transcendental, possibly transcendent or external analyses). This division may partly coincide with division between weak and strong paradoxes and between seeming and apparent paradoxes.²

According to Wójtowicz (2021) paradoxes hold an important place in philosophy—they force us to verify our beliefs and inspire us to search for new solutions. Still, there is a difference with TE since the paradoxes were not designed to resolve predefined problems and the conceivers may have been perplexed by them as well, so, they only conceived of new problems, new phrasings of problems instead of conceiving of resolutions for existing problems and they increased the number of problems instead of decreasing them.

Nevertheless, some philosophers define TE with reference to paradoxes, and we list the paradox view among picks of views in 2015 dissertation. Sorensen (1992) advances some theories, types and functions of TE, and his main theory seems to center around paradoxes “... A paradox is a small set of individually plausible yet jointly inconsistent propositions … every thought experiment is reducible to such a set. … They are the molds in which raw TE can be poured. They then enter the logician's mill...”. (Sorensen, 1992, p. 122)

However, Sorensen does not discuss the Liar in his main (1992) work on TE, it does not appear in the subject index, nor is Tarski discussed or does Tarski appear in the name index.

Sophistry, Huàtóus and Kōans

In earlier texts we have stressed possible ill intent of paradoxes, particular sophisms as used by sophists in ancient Greece  (see Kirk et al., 1983) a as they were made and intended to deceive (e.g. Achilles and the Tortoise), especially in contrast to Huàtóus and Kōans that have a predefined spiritual sense (that may have beneficial effects on health as well) and for that reason match out definition of TE better. (See Hertogh, 2018, on Vipassanā Meditation and Hertogh, 2021b, on Huàtóus and Kōans.)

Analyses

Orthodox Semantic Accounts

The Liar (or, let's say, Liar-type statements involving truth (predicates), self-reference as in the fields of conceptual analysis, semantics and set theory) rose to paradigmatic, revolutionary prominence by Tarski's Gödelian logicistic deliberations in the beginning of last century (Tarski 1933/1935,1983a, 1983b; Gödel, 1931, 2000), now considered the orthodox semantic account. This account remains within the correspondence theory (e.g., Aristotle, Augustine, Aquinas, Wittgenstein Tractatus). The Liar-type problem in these accounts does not consist in resolving the paradox, but in revising the logical system in such a way that the paradox will not occur anymore in the revision. It yielded Tarski's Convention T— 'p' [is true] iff p (e.g., 'ravens are black' [is true] if and only if ravens are black) (Tarski, 1933/1935, 1944, 1969, 1983b).

Text Analyses and Speech Act Accounts

Rise of semiotics and pragmatics in the second half of last century added textual analysis (Barthes, 1973, 2014, e.g. 'I am dead', derived from his analyses of an Edgar Allen Poe's story) and speech act accounts (Kearns, 2007; Epstein, 2015, Hoinarescu, 2018, lying as performative or counterformative speech act), revealing naturalist and ideal language biases.

Nonclassical Logical Accounts

Now nonclassical logical accounts may gain traction, revealing limitations and biases of standard logic. Matching our extended TE analyses, we mention some recent paracomplete and paraconsistent approaches to the Liar, which assume that the Liar may bring up for discussion logical principles like law of excluded middle (LEM P ∨ ¬P —Kripke, 1975, Beall at al. 2016/2023) and noncontradiction (LNC ¬(P ∧ ¬P) — Priest,1984; Karačić 2019), although we have to add that Kripke 1975 (e.g., $x (Px → Qx) ∧ Qx is ØT) may want to be considered classical logic,  possibly grounding logic in natural language, intuitions and kind of empirical observation sentences (Carnap, 1928, 1967), facts, state of affairs (Wittgenstein 1922, 1961). etc.

Beall et al. (2016/2023) argue that the Liar has formed 'the core of arguments against classical logic'--arguments for paracomplete logics (e.g. Kripke, 1975; Field, 2008) and paraconsistent logics (Asenjo, 1966; Priest,1984, 2006).

Beall et al. (2016/2023) discusses Kripke's Liar theory as 'most influential' example of a paracomplete approach to the Liar, where LEM fails 'ín some sense'. Liar sentences are neither true (T) nor false (F), but Kripke himself does not use an epithet like 'paracomplete' for his theory and writes about 'truth- value gaps' instead.

Priest (1979, 1984) proposes to accept the paradoxes as from a paraconsistent view on logic,

The purpose of the present paper is to suggest a new way of handling the logical paradoxes. Instead of trying to dissolve them, or explain what has gone wrong, we should accept them and learn to come to live with them. …For obvious reasons this will require the abandonment, or at least modification, of ‘classical’ logic... (Priest, 1979, p. 220)

Priest suggests accepting 'some sentences are true (and true only), some false (and false only), and some both true and false!' (Priest, 1979, p. 220).

The first version of the logic of paradox may already have been stablished in 1966 by Argentinian philosopher Florencio González Asenjo. Paraconsistent logics (term coined by Peruvian philosopher Francico Miró Quezada Cantuarias in 1976), and logics developed by Asenjo and Brazilian logician Newton Da Costa (Da Costa, 1974),  don't hold on to LNC in classical sense of 'ex contradictione sequitur quodlibet' ('from a contradiction, anything follows'), principle of explosion, but do allow for inconsistencies if not explosive and leading to triviality.

Saul Kripke

According to Kripke:

The versions of the Liar paradox which use empirical predicates already point up one major aspect of the problem: many, probably most, of our ordinary assertions about truth and falsity are liable, if the empirical facts are extremely unfavorable, to exhibit paradoxical features... (1975, p. 691)

Kripke does not mention many examples of 'extremely unfavorable' 'empirical facts' 'to exhibit paradoxical features,' (apart from 'Suppose, however, that Nixon's assertions about Watergate are evenly balanced between the true and the false, except for one problematic case', with regard to Nixon's Watergate scandal in 1972- 1974), but as Kripke advances a mathematical example of possible world (Kripke, 1980, 16--'The thirty-six possible states of the [two] dice are literally thirty-six ‘possible worlds,...’--see Hertogh 2021a), one might think of Quine's near-mathematical example of Frederic, reaching age of 21 after passing only five birthdays—since Frederic was born on February 29 (Quine, 1976, p. 1).

‘Seeking alternatives to the orthodox approach' (Kripke, 1975, pp. 698-700) since paradoxical sentences are 'ungrounded', they have 'truth-value gaps' and only 'partially defined predicates', choosing for Kleene's 'strong three-valued logic' (1952): Let us suppose that ØP is true (false) if P is false (true), and undefined if P is undefined.

However, in a note, Kripke (1975, pp. 700-701, note 18) adds the term “three-valued logic'” could be misleading and “our considerations can be formalized in a classical metalanguage”,

... I have been amazed to hear my use of the Kleene valuation compared occasionally to the proposals of those who favor abandoning standard logic ' for quantum mechanics,' or positing extra truth values beyond truth and falsity, etc. Such a reaction surprised me as much as it would presumably surprise Kleene, who intended (as I do here) to write a work of standard mathematical results, provable in conventional mathematics. ' Undefined' is not an extra truth- value …. Nor should it be said that ' classical logic' does not generally hold .... The term ' three-valued logic,' occasionally used here, should not mislead. All our considerations can be formalized in a classical metalanguage.

'Alternate Intuition'

According to Kripke (1975), paradoxes may be interpreted within a classical metalogical framework on at least an 'alternate intuition', which 'arises only after we have reflected on the process embodying the first intuition',

The approach adopted here has presupposed the following version of Tarski's ‘Convention T’, adapted to the three- valued approach: If 'k' abbreviates a name of the sentence A, T (k) is false, respectively iff A is true, or false. This captures the intuition that T(k) is to have the same truth conditions as A itself; it follows that T(k) suffers a truth- value gap if A does. An alternate intuition would assert that, if A is either false or undefined, then A is not true and T(k) should be false, and its negation true. On this view, T(x) will be a totally defined predicate and there are no truth-value gaps. Presumably Tarski's Convention T must be restricted in some way. (Kripke,1975, pp. 714-715 underline added)³

In note 35 he explains: “… I think the primacy of the first intuition can be defended philosophically, and for this reason I have emphasized the approach based on this intuition. The alternate intuition arises only after we have reflected on the process embodying the first intuition”. (Kripke, 1975, p. 715, note 35)

Also, Ripley (2013) wants to hold on to classical logic by extension of classical logic with 'a fully transparent truth predicate' and 'fully tolerant vague predicates'.⁴

Senselessness Etc. (Beyond Two Truth-values)

“I am somewhat uncertain whether there is a definite factual question as to whether natural language handles truth- value gaps- at least those arising in connection with the semantic paradoxes-...” (Kripke, 1975, p. 712) There are many more problems as in formalization of natural language that have triggered extensions of the logical systems but not revisions, such as:

A. Meaningless, senseless, nonsensical sentences, e.g., example of grammatical but 'nonsensical' sentence. “Colorless green ideas sleep furiously”, (Chomsky, 1957/2002, p. 15) which sentence also contains contradictions: colorless vs green. From beginning of development of modern logic, logicians, e.g., Wittgenstein (1922), have acknowledged that there are next to true (T) and false (F), 'meaningless', 'senseless', 'nonsense' sentences, which adjectives may amount to more than two truth-values, one or more extra truth-value.

According to Wittgenstein philosophical sentences are senseless (#4.003 – '.… Most propositions and questions, that have been written about philosophical matters, are not false, but senseless' [contrary to propositions of science], pseudo-propositions are senseless (#4.1272 '.…senseless pseudo-propositions ….'), laws of reference are senseless (#5.132 '…. Laws of inference, which-- as in Frege and Russell--are to justify the conclusions, are senseless and would be superfluous') and, famously, #6.54 'My propositions are elucidatory in this way: he who understands me finally recognizes them as senseless …').

'Meaningless' (Carnap, 1967), 'senseless' and 'nonsense' may be considered third truth-values (if not 'meaningless', 'senseless' third and 'nonsense', 'nonsensical' fourth truth-value etc.), similar to 'undefined', although the Liar-type sentences may be considered false because they do not exist in external reality as from a Wittgensteinian point of view (see also Kripke 'ungrounded').⁵

B. Truth in fiction (reference in fiction).

C. Tenses (temporal logic).

D. Metaphors (contextualism⁶), some say metaphors belong to another language game, they can't be fully translated into plain, literal language, some say sense and truth of metaphors are context dependent.

Finally, the question whether metaphors can be 'true', or rather 'fitting', 'correct' etc. According to Black [1954] metaphors belong to another language game than fact stating sentences, and as soon as there can be spoken of truth or falsehood there is no metaphor anymore, but literal, conventional use. Bartsch [1987] introduces a notion of context dependent truth, semantical meaningfulness. A sentence is semantical meaningful when the sentence is satisfied with respect to the referents of the referring constituents in that part of the discourse or situational setting. (Hertogh, 1989 – underline and bracketed remarks added)

E. More problems that have been resolved using alternate logics, that may be considered extensions to classical bivalent logic, such as deontic logic (logic of 'must', 'should' etc.), doxastic logic (logic of 'to believe' etc.), epistemic logic (logic of 'to know' etc.), modal logic (e.g., box and diamond operator), PWS (possible world semantics, in which symbolism, the aforementioned alternate logics could possibly be expressed).

F. Interjections, hesitations, mistakes, slips of the tongue, intonations etc., if not considered only emotional.

Above enumerated problems are studied in linguistics, logic, research projects of formalization of natural language. In fact, there are no deep problems here, since, although one may call for revisions, one eventually only adds extensions.

Falsification of Logical Laws

If the Liar wants to deny logical laws like LEM and LNC, the Liar could be formalized as the very denial, that is, negation of universal validity of these laws.⁷

                  With help of (metalogical) proposition logic, predicate logic and truth predicate Tx (x is True)

ØLEM                                                                                  [1]

Ø(P ∨ ØP)

Ø"x (Tx ∨ ØTx)                                                                 

∃x (Tx ∨ ØTx)

 

ØLNC                                                                                   [2]

ØØ (P ∧ ØP)

Ø"x Ø(Tx ∧ ØTx)

∃x Ø (Tx ∧ ØTx)

Communicative Account Proposal

About the semantic versions of the Liar, we propose a pragmatic Gricean account, analyzing Epimenides's version of the Liar as falsification of generic tacit conversational principle—violation of Grice (1975) maxim of quality and maxim of manner--that people usually speak truth and perspicuously. By application of TE Matrix Epimenides-style paradox is extended to a valid and sound modus tollens argument (Popper, 1935, 1959/2002) with logical force of enthymeme (Aristotle, 1924). Maxims of quality and manner are derived from Grice Cooperative Principle (Grice, 1975, pp. 45-47):

Cooperative Principle (CP): Make your conversational contribution such as is required, at the stage at which it occurs, by the accepted purpose or direction of the talk exchange in which you are engaged.

Maxim of QUANTITY: quantity of information:

1.  Make your contribution as informative as is required (for the current purposes of the exchange).

2.  Do not make your contribution more informative than is required

Maxim of QUALITY: Try to make your contribution one that is true:

1.  Do not say what you believe to be false.

2.  Do not say that for which you lack adequate evidence.

Maxim of RELATION, relevance: Be relevant.

Maxim of MANNER: Be perspicuous.

1.   Avoid obscurity of expression.

2.  Avoid ambiguity.

3.  Be brief (avoid unnecessary prolixity).

4.  Be orderly.

Logical Analyses

Maxim of quality, people usually speak truth⁸, and maxim of manner, people usually speak perspicuously, are not just moral rules but empirical rules—if not, communication will be hampered. We can't deny (effective) communication is well possible, it runs the world, so, we may assume people indeed usually speak truthful and perspicuously.

We may apply (part of) apparatus to formalize natural language as with help of predicate logic.

Suppose

Cx                               x is a Cretan

Sx                              x Speaks (truth)

Lx                              x Lies (do not speak truth)

X                                 person(s), human(s) (variable)

a                                 a definite, specific person, e.g., Epimenides (constant)

"x                               universal quantifier, for all x it holds that...

∃x                               existential quantifier, for some, at least one, x it holds that …

∃!x                                       unique existential quantifier, for exactly one x it holds that

∧                                 conjunction

®                                (material) implication

Ø                                 negation

There is exactly one Cretan who says 'All Cretans are liars'.⁹

Which is the raw still invalid and unsound TE, bracketed in TE Matrix methodology

 

 

 

 

 

 

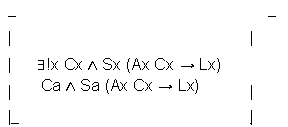
TE analyses may yield next valid and sound argument

P₀                                  Ax (Cx → Sx)

P₁                                  Ca ∧ Sa (Ax (Cx → Lx))

P₂                                  ∃!x Cx ∧ Sx (Ax (Cx → Lx))

P₃                                  Lx ↔ ØSx

P₄                                  ∃!x Cx ∧ Sx (Ax (Cx → ØSx))

 

P₅/C                              Ø(Ax (Cx → Sx))

Or shortly:

P'₀ "x (Cx → Sx)                 Grice´s maxim of quality P'₁

Ca ∧ Sa (Ax (Cx → ØSx))  Epimenides Liar paradox

P'₂/C    Ø"x (Cx → Sx)

It is about falsification of generic tacit conversational principle –Grice (1975) maxim of quality– that people usually speak truth, amounting to a valid and sound modus tollens argument (e.g. Popper, 1935, 1959/2002) with logical force of enthymeme (e.g. Aristotle,1924); falsification of generic rules by counterexamples (e.g. paradoxes) may be formalized as modus tollens (according to Popper, 1935, 1959/2002), and formula [4] may not exactly match the structure of modus tollens (P → Q, ØQ, therefore ØP), but it is reducible to it.

We could add it is not (only) about violating of maxim of quality, but (also) about violating of maxim of manner (e.g. on antinomic interpretations of the paradox)—apart from false, the Liar-type statements may (also) be considered paradoxical, that is in terms of the 4th maxim – obscure and ambiguous.

Also Eubelids’ version, 'This statement is false' [d], interpreted as an antinomy leads to conflicting inferences (if d is true, then d is false; if d is false, then d is true – see note 2), which is a kind of strong ambiguity and obscurity, if not contradiction, and therefore it violates maxim of manner, defect of clarity, perspicuity, confusing of zero and metalevel; and one may as well say that it is false, violating maxim of quality.

Interpretations (Conclusions)

 

1.    Although paradoxes and antinomies like Liar-type statements don't live up to all conditions of TE definition (they particularly fail the pragmaticist condition), they may be analyzed and interpreted with help of TE methodology of TE Matrix (logically analyzed as Extended Arguments) and TE Diagram (surveys).

2.    The Liar, e.g., on Tarski's orthodox account, is a paradigmatic mathematical strong thought experiment, that as a paradox may be considered a metalogical instrument that questions its very presuppositions or the presuppositions of the logical system it is part of. We may particularly discuss semantic (instead of set theoretical) versions, such as Epimenides' (7th-6th cent. BCE) and Eubulides' (4th cent. BCE).

3.    About discussions about classical logic and nonclassical logic as three-valued logics in attempts to resolve Liar-type paradoxes. We show that there are already more than two 'truth-values' used in the logical systems of Rudolf Carnap, Bertrand Russell, Ludwig Wittgenstein Tractatus—next to T(rue) and F(alse), respectively,  'meaningless'; nonsense, just a noise without meaning; 'nonsense' ('unsinnig'), 'senseless' ('sinnlos'). For the moment we may conclude that laws of logic, such as LEM and LNC, may have lost their categorical, apodictic status.

4.    We propose a Gricean account of breaching of communicative norms, analyzing Epimenides's version of the Liar (The Cretan says, 'All Cretans are liars') as falsification of generic tacit conversational principles –Grice (1975) maxim of quality and maxim of manner– that people usually speak truthful and perspicuously. This analysis may also hold for Eubulides-type Liar paradoxes as 'this sentence is false', since the very statement violates Grice's maxims of manner and quality, it is obscure, ambiguous (for directly or indirectly paradoxical), if not false. Thus, by application of TE Matrix, Epimenides-style and Eubulides-style paradoxes can be extended to valid and sound modus tollens arguments (Popper, 1935, 1959/2022) with logical force of enthymeme (Aristotle, 1924).

5.    Historical interpretations of most renowned modern logicians show a variety of views on the Liar- type paradoxes. Russell considers the set theoretic Russell's Paradox and semantic Barber Paradox nonsense—“... the whole question whether a class is or is not a member of itself is nonsense ... because the whole form of words is just a noise without meaning.” (Russell, 1919, p. 355). In Tractatus #3.24 Wittgenstein may have shown a classical logical resolution of Liar-type paradoxes, holding that propositions about complexes, which do not exist, are 'not nonsense but simply false.' Kripke (1975) nonclassical view involving (Kleene's) three truth-values ('ungrounded' paradox, so no truth-value applicable, but “undefined”) may be interpreted within a classical metalogical framework on at least an “alternate intuition” as Kripke himself contends—"The term 'three-valued logic', occasionally used here, should not mislead. All our considerations can be formalized in a classical metalanguage” ( Kripke, 1975, p. 701, note, 18). Textual analyses, semiotics, and speech act theory add a plethora of examples of paradoxical self- reference focusing on analyses of 'lying'. Neoclassical accounts, accepting paradoxes as 'brute facts' (Priest, 1979) may develop paracomplete and paraconsistent analyses assuming breaching of resp. LEM and LNC. Since there is no communis opinio the Liar may remain a conundrum. As we may have shown by a Gricean account a two-valued classical logical resolution is possible but LEM and LNC may have lost their status of categorical universal truth. In terms of Sorensen (1992) the Liar could be considered a necessity refuter TE, and after Tarski (1933/1935,1969, 1983a, 1983b) a crucial consistency test TE. It could be visualized by Necker cube (Wittgenstein perceptual ambiguity), or a Penrose tribar (or triangle) (perceptual impossibility), what Hofstadter could call a feedback loop, related to core of consciousness (Hofstadter, 1979/1999, 2007), possibly rather the beginning than the end of human formalization attempts.

6.    TE Diagram survey during and after conference Perspectives of Truth 2 in Bucharest (RO/EU), September 29, 2023, shows that LEM scores far lower (0.6) than Pythagorean Theorem (1.0) and Einstein's Relativity (0.9), possibly indicating that there is less academic confidence in classical logic nowadays (results of TE Diagram are not statistically significant since n =10). See Hertogh (2022) for more explanation and examples of TE Diagram surveys.

7.    Possibly a rather farfetched speculative implication. We have followed extension option in this paper but on a strong interpretation of Liar-type sentences, they may show that there could be a mismatch between axiomatized mathematical systems and human and nonhuman reality of Planet Earth, and fundamental revisions may be needed. For this reason, among more reasons, we advocate a Descriptive Semantics View, instead of an axiomatized prescriptive system, without a forcing valuation function (still extension or methodological modesty than revision). For this reason, one could try and replace mathematics with another foundational discipline and science, e.g., linguistics (Wittgenstein Philosophical Investigations), biology (evolutionary epistemology), and ecology (end of Anthropocene). One may even argue that there is also a mismatch between mathematically based natural science and human and nonhuman reality of Planet Earth, which may eventually result in mismatches between natural science theory and reality, like we suffer now in the climate crisis, resulting from irresponsible technological societal applications of natural science theories, that have already been proven many times to be harmful to (wo)man and nature, human health and global ecology (environmental pragmaticist 21st century condition of semantics of thought experiments).

8.    We may express global cross-cultural and environmental pragmaticist concerns by an addition to Popper's formula of progress of science (Popper, 1979, p. 243), thereby modifying it into Progress of Science and Society View

P₁     →       TS          →                     EE/EP GC       →       P₂

Problem → Tentative Solutions → Error Elimination → Problem

situation 1                                                                             situation 2

In the 21st century Error Elimination (EE) could focus on Environmental Pragmaticism (EP) (countering pollutive effects of technological societal applications of science) and Global Cross-culturalism (GC) (theories should hold for, say, at least two cross-cultural communities). (Hertogh, 2015, 2018, 2020)

Acknowledgements

The research into antinomies of the Liar has benefited from academic presentations at two conferences in 2023, Perspectives About Truth 2, organized by Politehnica University of Bucharest (RO/EU), September 29-30, 2023, special thanks to Paula Tomi, and Workshop New Perspectives on Anomalies in the Sciences, organized by Universidade Federal do Rio de Janeiro (BR), October 5-6, 2023, special thanks to María del Rosario Martínez-Ordaz).

Notes

 

¹ Or, gender neutral, does a hairdresser who dresses hair of all those, and those only, who do not dress their hair themselves, dress her/his hair?

² There are many types and taxonomies of paradoxes, e.g., seeming or apparent paradoxes, that may be resolved on analyses, direct paradoxes (contradictions) and indirect paradoxes (antinomies). Liar-type sentences are often antinomies, where there is a conflict or contradiction between inferences drawn from a paradoxical sentence, e.g., Eubelids’-style

This statement is false.                                                                    [d]

Inference 1:

Suppose [d] is true, then it is, in fact, false (contradiction)

Inference 2:

Suppose [d] is false, then it is, in fact, true (contradiction)

In accordance with definition in Paradoxes section, it is about intermingling of zero and meta level, possibly similar to what Hofstadter (1979/1999) calls feedback loops, possibly similar to kōans, visualized by optical illusions and impossible objects, such as Necker cube (see note 5, Tractatus #5.5423) and Penrose tribar etc., of which Penrose says 'It is clear that the ''3-dimensional object'' which the drawing [of a Penrose tribar] apparently depicts cannot exist in ordinary Euclidean space' (Penrose, 2004, p. 992) and '(An impossible object is a drawing of a solid figure that cannot exist because it embodies self- contradictory elements)' (Penrose, 1989, p. xv). See also note 5, Wittgenstein on Necker cube), and visit https://ia801208.us.archive.org/6/items/RoadToRealityRobertPenrose/road%20to%20reality-robert%20penrose.pdf PDF version of Penrose, 2004, The Road to Reality, which shows Penrose Tribar, as an example of an 'impossible object', to top of p. 992, fig. 33.21, Ch. 33, §33.9. (See also Hertogh, 2018, p, 269, note 7; Hertogh, 2021b, on Huàtóus and Kōans.) Hertogh (2025), on Dao De Jing, p. 54, figure 4, Penrose triangle – Source: https://en.wikipedia.org/wiki/List_of_optical_illusions

³ Kripke seems to be unsure about the truth-gap approach and natural language

On the basis of the fact that the goal of a universal language [e.g., Tarski] seems elusive, some have concluded that truth-gap approaches, or any approaches that attempt to come closer to natural language than does the orthodox approach, are fruitless. I hope that the fertility of the present approach, and its agreement with intuitions about natural language in a large number of instances, cast doubt upon such negative attitudes. (Kripke, 1975, p. 715)

I am somewhat uncertain whether there is a definite factual question as to whether natural language handles truth- value gaps- at least those arising in connection with the semantic paradoxes. (Kripke, 1975, p. 712)

⁴Ripley:

This paper provides a defense of the full strength of classical logic, in a certain form, against those who would appeal to semantic paradox or vagueness in an argument for a weaker logic.

I will not argue that these paradoxes are based on mistaken principles; the approach I recommend will extend a familiar formulation of classical logic by including a fully transparent  truth predicate and fully tolerant vague predicates. It has been claimed that these principles are not compatible with classical logic; I will argue, by both drawing on previous work […] and presenting new work in the same vein, that this is not so. We can combine classical logic with these intuitive principles, so long as we allow the result to be nontransitive. In the end, I hope the paper will help us to handle familiar paradoxes within classical logic; along the way, I hope to shed some light on what classical logic might be for. (2013 , p. 1, underline added)

⁵ Wittgenstein also mentions theory of probability with many truth-values, example of many- valued logic “4.464 The truth of tautology is certain of propositions possible, of contradiction impossible. (Certain, possible, impossible: here we have an indication of that gradation which we need in the theory of probability.) (Wittgenstein, 1961, p. 54)

In Russell's Wittgenstein interpretation sentences about ethics are 'mystical' or 'inexpressible' (possibly again additional truth-values)--see Wittgenstein (1922, p. 18) from introduction by Russell:  “…. The whole subject of ethics, for example, is placed by Mr Wittgenstein in the mystical, inexpressible region...”. However, we could possibly assume antinomies as the Liar may be considered complex and non-existent and are therefore not nonsense but false (similar to Kripke's 'alternate intuition'). Every statement about complexes can be analysed into statements about their constituent parts (#2.0201); in case of the Liar, the proposition appears to be complex because of its reference that is equivocal, ambiguous--non-existent (#3.24, similar to Kripke's 'ungrounded'), possibly similar to Necker Cube perceptual ambiguity (#5.5423)

3.24      A complex can only be given by its description, and this will either be right or wrong. The proposition in which there is mention of a complex, if this does not exist, becomes not nonsense but simply false.... (Wittgenstein, 1922, p. 33)

5.5423 To perceive a complex means to perceive that its constituents are combined in such and such a way. This perhaps explains that the figure

[image Necker cube with letters added]

can be seen in two ways as a cube; and all similar phenomena. For we really see two different facts. (If I fix my eyes first on the [lower] corners a and only glance at [higher] b, a appears in front and b behind, and vice versa.) (Wittgenstein, 1922, pp. 71-72, bracketed remarks added)

Visit https://www.gutenberg.org/files/5740/5740-pdf.pdf Gutenberg version of Tractatus, which shows Necker cube, and letters added by Wittgenstein, on p. 72 and German text on p. 142; see also Hertogh (2025), p. 54, figure 3, Necker cube--without any numbers--Source: https://en.wikipedia.org/wiki/List_of_optical_illusions).

Daniel Rowe (Oxford University) remarked during conference Perspectives about Truth 2 that Wittgenstein does not think the Liar is a philosophical important problem, but that Kripke does. For more Kripkean takes of the Liar, see Rowe, 2023, 'Temporal or Staged Logic and the Disambiguation of Semantic Paradoxes.' Remarks on use of 'senseless' and 'nonsense' in Tractatus are based on Ogden/Ramsey translation (Wittgenstein,1922 – preferring 'senseless') and could be double-checked by more translations (as Pears/McGuinness, Wittgenstein, 2022 – preferring 'nonsensical') and German original (Wittgenstein, 1922, 2022 -- 'sinnlos' and more often 'unsinnig'), but it may result in same conclusion viz. that there are used more than two truth-values in Tractatus.

⁶ We don't think contextualism may entail relativism, rather relativity, saying that different parts, domains of reality are formalized in a different way. In analyses of metaphors (Hertogh, 1989) we distinguish between standard semantic metaphors and context-dependent or pragmatic metaphors. The latter may be identified, analysed and formalized with help of thematic dimensions, a semantic term for context; in case of metaphors, it is most often about the actual context, that is the sentence in which the metaphor theme appears. Different parts of reality (domain, discourse etc.) may be analysed and interpreted different as in accordance with possibly different structure, texture, substrate etc. of different parts of reality, logic may not only study declarative sentences (Wittgenstein, 1922, Russell & Whitehead, 1910-1913; Carnap, 1928, 1967), but many more moods, such as questions, irony etc. (Wittgenstein, 1953; Searle, 1969; Grice, 1975, etc.). E.g. Galileo's gravity theory may hold (by approximation) for Planet Earth, Einstein's relativity theory for micro- and macrocosm. Voodoo and Hollywood Zombies should be analysed different from p- or philosophical Zombies (see Chalmers, 2017; Hertogh, 2023c). Poetical metaphors may be analysed different from philosophical metaphors, the former may be close to similes, the latter are often a tip of a (theoretical) submerged model. It would be a kind of word magic to suggest that a word may mean the same in each context. Historical and etymological research may show how word meanings develop by metaphorical and metonymical extensions, whereby substantial use of a word in a new context may result in a new (dictionary) sense.

⁷ LEM, LNC go back on Aristotle, On Interpretation, Metaphysics (Aristotle, 1908-1952). These basic logical laws appear in more cultures, e.g., in Mohist logic as 'basic principles regulating disputations' (see Zhang & Liu, 2007).

⁸ Martinich compares Grice's maxim of quality to Searle's sincerity condition (Martinich, 1980, p. 226). Fallis tries to define and categorize instances of lying (Grice--'Do not say what you believe to be false') in terms of intentions, beliefs, misspeakings, sarcasms, unawareness, insincere assertions, and concludes it is about violating a norm: “Even so, all liars, including young children, do intend to communicate something false by saying that thing. Thus, they do intend to do something that would violate the norm against communicating something false if it were in effect”. (Fallis, 2012)

It takes half a century from Richard Nixon's exceptional Watergate scandal lying (discussed in  Kripke, 1975) to David Trump's allegedly habitual lying in 2010s, 2020s. One may wonder, isn't the present-day USA President breaching Grice's maxims? And an answer could be that the fact that the President is allegedly lying, is communicated to him and exposed in media and academics (Hoinarescu, 2018) continuously, called fact checking, which may prove Grice's maxims are still alive today, and that there have been introduced terms like misinformation and disinformation—next to President's disparagement of the media as fake news--to handle a situation of possibly increasing false, misleading and biased information in communication of governments, companies, social media etc., whether or not one may reduce these discussions to community debates only (e.g., Facebook). (See Broda & Strömbäck, 2024, concluding 'Considering the threat misinformation, disinformation, and fake news pose, it is vitally important that we … continue advancing the field. The stakes are undoubtedly high (p. 161).)

Critical thinking could help deciding whether a claim is always true, sometimes true, partly true, or false (see Hertogh, 2015, p. 64, section on logic and critical thinking, pp. 60-74; see also Hertogh, 2022).

⁹ With regard to possibly uniquely defining existential quantification– It is more likely that Epimenides (or any other one Cretan) is lying than that all Cretans are lying, isn't it? (as depending on your presupposition whether or not you think people usually speak truth, or are usually lying, which is in fact exemplified with regard to Cretans in P₀/P'₀).

Falsification –so, it is not surprising that according to Gödel and Tarski these exceptions may falsify parts of arithmetic, logic, mathematics as a consistent and coherent system.

References

Anapolitanos, D. A. (1991). 'Thought Experiments and Conceivability Conditions.' In T. Horowitz, & G. Massey (Eds.) Thought Experiments in Science and Philosophy. Rowman and Littlefield (pp. 87-98). https://philsci-archive.pitt.edu/3190/1/thought_experiments_toc.htm

Aristotle. (1908-1952). The Works of Aristotle, Translated into English Under the Editorship of W.D. Ross, 12 Vols. Clarendon Press.

Aristotle. (1924). Rhetorica, The Works of Aristotle, Vol. 11 (Trans. Roberts, W. Rhys). Clarendon Press.

Asenjo González, F. (1966). A Calculus of Antinomies. Notre Dame Journal of Formal Logic, 7(1), 103-105.

Barthes, R. (1973). Analyse textuelle d'un conte d'Edgar Poe. In C. Charbrol, Sémiotique narrative et textuelle (pp. 29-54). Librairie Larousse.

Barthes, R. (2014). The Death of the Author Textual Analysis: Poe's ''Valdemar''.' (Trans. G. Bennington). In D. Lodge,  & N. Wood (Eds.) Modern Criticism and Theory: A Reader (pp. 311-336, Ch. 17). Third Ed. Routledge.

Bartsch, R. I. (1987). Norms of Language, Theoretical and Practical Aspects. Longman.

Beall, Jc., Glanzberg, M., & Ripley, D. (2016/2023). Liar Paradox. Stanford Encyclopedia of Philosophy (Winter 2023 Edition), Edward N. Zalta & Uri Nodelman (Eds.).

Black, M. (1954). Metaphor. Proceedings of the Aristotelian Society, 55, 273-294.

Broda, E., & Strömbäck, J. (2024). Misinformation, Disinformation, and Fake News: Lessons from an Interdisciplinary, Systematic Literature Review. Annals of the International Communication Association, 48.(2), 139–166. https://doi.org/10.1080/23808985.2024.2323736

Carnap, R. (1928). Der logische Aufbau der Welt. Felix Meiner Verlag.

Carnap, R. (1967). The Logical Structure of the World Pseudoproblems in Philosophy. (Trans. R. A. George). University of California Press.

Chalmers, D. J. (2017). Zombies on the Net. https://consc.net/zombies-on-the-web/

Chomsky, N. (2002). Syntactic Structures, Second Edition with an Introduction by David W Lightfoot. Mouton de Gruyter. (Original work published 1957)

Da Costa, N. C. A. (1974). On the Theory of Inconsistent Formal Systems. Notre Dame Journal of Formal Logic, 15(4), 497–510.

Einstein, A., & Infeld, L. (1938). The Evolution of Physics-From Early Concept to Relativity and Quanta. Cambridge University Press.

Epstein, M. (2015). 'Paradoxical Speech Acts: Transformatives and Counterformatives.' Parallax, 21 (2), 134-142.

Fallis, D. (2012). Lying as a Violation of Grice's First Maxim of Quality. Dialectica, 66(4), 563-581.

Galileo G. (1638/1914). Mathematical Discourses and Demonstrations, Relating to Two New Sciences/Dialogues concerning Two New Sciences, Translated from the Italian and Latin into English by Henry Crew and Alfonso de Salvio. With an Introduction by Antonio Favaro (Trans. Galileo 1638. Discorsi e Dimostrazioni Matematiche, Intorno à Due Nuove Scienze. Elsevirii). MacMillan.

Gödel, K. (1931). Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, I. Monatshefte für Mathematik und Physik, 38, 173–98.

Gödel, K. (2000). On Formally Undecidable Propositions of Principia Mathematica and Related Systems. Translated by B. Meltzer, Introduction by R.B. Braithwaite. Dover Publications.

Grice, H. Paul (1975). Logic and Conversation. In P. Cole, & J. Morgan (Eds.) Syntax and Semantics Vol.3 Speech Acts (pp. 41-58). Academic Press.

Hertogh, C. P. (1989). Identification, Analysis, and Interpretation of Metaphorical Indicative Sentences of Subject-Predicate Form. Trans. Conclusion Unpublished Master's Thesis University of Amsterdam.

Hertogh, C.P. (2015). Semantics of Thought Experiments. PhD diss. VUB Brussels.

Hertogh, C.P. (2018). Logical Analyses of Vipassanā Meditation. Contemporary Buddhism, 19 (2), 251-271.

Hertogh, C.P. (2020). Goodman’s Grue—Relativized Pluralism and Paradigmatic Thought Experiment (Whack). Humanities Bulletin, 3(1), 64-103.

Hertogh, C.P. (2021a). Computation and Visualization Thought Experiments after Lakatos's Heuristic Guessing Method. In M. Trepczyński (Ed.) Philosophical Approaches to the Foundations of Logic and Mathematics in Honor of Professor Stanisław Krajewski (pp, 271-297, Ch. 10). Leiden.

Hertogh, C.P. (2021b). Thought Experiment Analyses of Huàtóus and Kōans. In Rivas, V. (Ed.), (2021). PAP Transactions (pp. 93-107). 2nd USAPP Summit, July 21-24.

Hertogh, C.P. (2023a). Thought Experiment Analyses of the Liar. Presentation Perspectives about Truth 2, September 29-30, 2023, Bucharest.

Hertogh, C.P. (2023b). Semantics of the Liar. Presentation Workshop New Perspectives on Anomalies in the Sciences, October 5-6, 29-30, 2023, Rio de Janeiro.

Hertogh, C.P. (2023c). The Conceivability of Consciousness--Kirk’s and Chalmers’s Zombie Thought Experiments. London Journal of Research in Computer Science and Technology, 23(1), 21-41.

Hertogh, C.P. (2024). Thought Experiment Analyses of Albert Einstein's Elevator [Análisis del experimento mental del elevador de Albert Einstein]. Analítica (4), 10-40.

Hertogh, C.P. (2025). Predication and Opposition in Dào Dé Jīng Thought Experimental Analyses of 道可道非常道(III)– Global Cross-cultural and Religious Aspects, Humanities Bulletin, 8(1), 20-56.

Hofstadter, Douglas R. (1999). Gödel, Escher, Bach: An Eternal Golden Braid. Basic Books. (Original work published 1979)

Hofstadter, D. R. (2007). I Am a Strange Loop. Basic Books.

Hoinarescu, L. (2018). Lying as Speech Act. A Sociodiscursive and Interactional Approach. Revue Roumaine de Linguistique, 63 (1–2),  147–166.

Horowitz, T. & Massey, G. J. (Eds.). (1991). Thought Experiments in Science and Philosophy. Rowman and Littlefield. https://philsci-archive.pitt.edu/3190/1/thought_experiments_toc.htm

Kearns, J. (2007). An Illocutionary Logical Explanation of the Liar Paradox. History and Philosophy of Logic, 28, 31–66.

Kirk, G.S., Raven, J. E., & M. Schofield (1983). The Presocratic Philosophers: A Critical History with a Selection of Texts (Second Edition). Cambridge University Press.

Kleene, S. C. (1952). Introduction to Metamathematics. Van Nostrand.

Kripke, S. A. (1975). Outline of a Theory of Truth. Journal of Philosophy, 72, 690–716. Reprinted in Martin, R. L. (Ed.). (1984). Recent Essays on Truth and the Liar Paradox (pp. 54-81). Clarendon.

Kripke, S.A. (1980). Naming and Necessity. Basil Blackwell.

Kripke, S.A. (1982). Wittgenstein on Rules and Private Language. Harvard University Press.

Kripke, S.A. (2019). 'Naming and Necessity Revisited.' Center for Logic and Language Special Lecture May 30, 2019, Institute of Philosophy, University of London. [Video] https://www.youtube.com/watch?v=3zazonG6zBk

Kuhn, T. S. (1970). The Structure of Scientific Revolutions. Enlarged Second Ed. (First Ed. 1962) University of Chicago Press.

Martinich, A. P. (1980). Conversational Maxims and Some Philosophical Problems. The Philosophical Quarterly, 30(120), 215-228.

Martin, R. L. (Ed.). (1970). The Paradox of the Liar. Yale University Press.

Martin, R.L. (Ed.). (1984). Recent Essays on Truth and the Liar Paradox. Clarendon Press.

Penrose, R. (1989). The Emperor's New Mind: Concerning Computers, Minds and The Laws of Physics. Oxford University Press.

Penrose, R. (2004). The Road to Reality, A Complete Guide to the Laws of the Universe. Jonathan Cape: London. https://ia801208.us.archive.org/6/items/RoadToRealityRobertPenrose/road%20to%20reality- robert%20penrose.pdf

Popper, K. R. (1935). Logik der Forschung. Julius Springer Verlag.

Popper, K.R. (2002). The Logic of Scientific Discovery, Translation by the Author of Logik der Forschung 1935. Routledge Classics. (Original work published 1959)

Popper, K.R. (1979). Objective Knowledge: An Evolutionary Approach, Revised Edition. (First Ed. 1972) Clarendon Press.

Priest, G. (1979). Logic of Paradox. Journal of PhiIosophical Logic, 8, 219-241.

Priest, G. (1984). Logic of Paradox Revisited. Journal of Philosophical Logic, 13(2), 153–179.

Quine, W.V.O. (1976). Ways of Paradox. Harvard University Press.

Ripley, D. (2013). Revising up: Strengthening Classical Logic in the Face of Paradox. Philosophers’ Imprint, 13(5), 1-13.

Rowe, D. (2023). Temporal (or Staged) Logic and the Disambiguation of Semantic Paradoxes. Presentation Perspectives about Truth 2, September 29-30, 2023, Bucharest.

Russell, B. (1919). The Philosophy of Logical Atomism, VII The Theory of Types and Symbolism: Classes, VIII Excursus into Metaphysics: What There Is. The Monist, 29 (3), 345–380.

Russell, B. & Whitehead, A. N. (1910–1913). Principia Mathematica. 3 Vols. Cambridge University Press.

Searle, J. R. (1969). Speech Acts: An Essay in the Philosophy of Language. Cambridge University Press.

Sorensen, R. A. (1992). Thought Experiments. Oxford University Press. http://course.sdu.edu.cn/G2S/eWebEditor/uploadfile/20121224164821178.pdf

Sutrop, U. (2009). Wittgenstein’s Tractatus 3.333 and Russell’s Paradox. Trames, Journal of the Humanities and Social Sciences, 13(2), 179–197. https://doi.org/10.3176/tr.2009.2.06

Tarski, A. (1969). Truth and Proof. Scientific American, 220 : 63–77 (63-70, 75-77).

Tarski, A. (1935). Der Wahrheitsbegriff in den formalisierten Sprachen (L. Blaustein, transl., with a postscript added), Studia Philosophica, 1, 261–405. [Original work published 1933]

Tarski, A. (1944). The Semantic Conception of Truth: And the Foundations of Semantics. Philosophy and Phenomenological Research, 4(3), 341–375.

Tarski, A. (1983a). Logic, Semantics, Metamathematics. (Second Ed.) (J. Corcoran, Ed.). Hackett.

Tarski, A. (1983b). The Concept of Truth in Formalized Languages. (J. H. Woodger, Transl.), in A. Tarski, Logic, Semantics, Metamathematics (Second Ed., pp. 152-278).). Hackett.

Wittgenstein, Ludwig (1922). Tractatus Logico-Philosophicus. With an Introduction by Bertrand Russell. Trans. C. K. Ogden. (Bilingual Ed.) Kegan Paul Trench Trubner. https://www.gutenberg.org/files/5740/5740-pdf.pdf [eBook #5740]

Wittgenstein, L. (1953). Philosophical Investigations. Basil Blackwell.

Wittgenstein, L. (1961). Tractatus Logico-Philosophicus. Trans. McGuinness, B.F. and D.F. Pears, and with Introduction by Bertrand Russell. The Humanities Press.

Wittgenstein, L. (2022). Tractatus Logico-Philosophicus Logisch-philosophische Abhandlung by Ludwig Wittgenstein (First published by Kegan Paul London, 1922) Side-by-side-by-side Edition, Version 0.63 (July 14, 2022) containing the original German, alongside both the Ogden/Ramsey, and Pears/McGuinness English translations. https://people.umass.edu/klement/tlp/

Wójtowicz, A. (2021). An Analysis of Paradoxes. In M. Trepczyński (Ed.) Philosophical Approaches to the Foundations of Logic and Mathematics in Honor of Professor Stanisław Krajewski (pp, 258-270).  Leiden.

Zhang, J. & , Liu, F. (2007). Some Thoughts on Mohist Logic. In J., van Benthem, S. Ju, & F. Veltman (Eds.)(2007). A Meeting of the Minds: Proceedings of the Workshop on Logic, Rationality and Interaction. College Publications (pp. 85-102) . https://www.researchgate.net/publication/240798715_Some_Thoughts_on_Mohist_Logic