Derechos de autor 2024 Tecnociencia
Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-CompartirIgual 4.0.
Desde los cursos de cálculo diferencial se sabe que una función continua no necesita ser diferenciable; sin embargo, se tiene la idea errónea que una función continua tiene que ser diferenciable en muchos puntos. Con la idea de corregir este error, en el presente artículo se construye un ejemplo de una función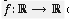 
que es continua y no diferenciable en todo punto 
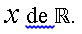También se prueba que el conjunto de puntos de continuidad de la derivada de una función diferenciable es enumerable. Además, se presenta un ejemplo de una función diferenciable cuyo conjunto de discontinuidad de la derivada es denso.
Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.
