Copyright (c) 2024 Tecnociencia
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
From differential calculus courses it is known that a continuous function need not be differentiable; however, there is a mistaken idea that a continuous function must be differentiable at many points. With the idea of correcting this misconception, in this paper an example of a function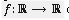 
that is continuous and nowhere differentiable in is constructed. It is also proved that the set of point where the derivate of a differentiable function is continuous is enumerable. Furthermore, an example of a differentiable function whose set of discontinuity of the derivate is dense.
Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.
