Derechos de autor 2024 Tecnociencia
Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-CompartirIgual 4.0.
Se programó una herramienta digital para utilizarse en línea y gratuita, a través de la plataforma Geogebra. Dicha herramienta resuelve numéricamente la ecuación de Laplace con valores en la frontera (del tipo Dirichlet) para una malla rectangular de 6×6, en la que 20 valores están en la frontera y 25 valores están en el interior, todos distribuidos de manera uniforme en coordenadas cartesianas. El método numérico utilizado para resolver la ecuación diferencial fue el método de diferencias finitas, en el cual se apreció que, para calcular cada valor del campo escalar “ui,j” dentro de la malla rectangular, se realizó el promedio de los valores adyacente al valor en cuestión, es decir
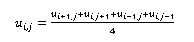
Por otro lado, para plantear el grado de aproximación entre el modelo analítico “MA” (la ecuación de Laplace) y el modelo numérico “MD” (método de diferencias finitas) se realizó una expansión en serie de Taylor, hasta el quinto término, de un valor arbitrario “u(x,y)” del campo escalar, con lo que dicho planteamiento llega al siguiente resultado
En donde el término “TD” es denominado “término de discrepancia”, ya que el mismo marcó la diferencia cuantitativa entre dichos modelos matemáticos. Su forma analítica obtenida fue la siguiente
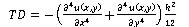
El término “h” representó la forma en que había sido seccionado la malla. Adicional a esto, si el campo escalar variaba de manera suave y las condiciones en la frontera eran homogéneas, se podía obtener una solución general para la ecuación diferencial de Laplace. En dicha solución, se generaron constantes que dependían de las condiciones de frontera, con lo que se desveló, para un sistema físico estable en concreto, la dependencia del TD con el cuadrado de h.
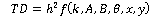
Resaltó a la vista, el hecho de que al hacer el término h más pequeño, este término de discrepancia se volvió irrelevante y consecuentemente, ambos modelos, analíticos y numérico, mostraron su aproximación.
Para resolver el sistema lineal de ecuaciones de primer grado, se utilizó la regla de Cramer. Para la creación del algoritmo se utilizó el software Geogebra Clásico, Versión 6.0.801.0, el cual es gratuito. El link para acceder a esta herramienta digital es la dirección web, https://www.geogebra.org/m/rmwrxxsa. El objetivo de la creación de esta herramienta estuvo basado en el estudio de sistemas físicos bajo condiciones de equilibrio o estables, tales como: el flujo térmico estable sobre una lámina conductora, una distribución estática de potencial eléctrico sobre una superficie, una distribución de presión que describe el flujo estable de un fluido, etc.
Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.
