Copyright (c) 2024 Tecnociencia
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
A digital tool was programmed to be used online and free, through the Geogebra platform. This tool numerically solves the Laplace equation with values ??on the boundary (of the Dirichlet type) for a 6×6 rectangular mesh, in which 20 values ??are on the boundary and 25 values ??are inside, all distributed uniformly in Cartesian coordinates. The numerical method used to solve the differential equation was the finite difference method, in which it was noted that, to calculate each value of the scalar field “ui,j” within the rectangular mesh, the average of the values ??adjacent to the value in question, that is
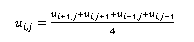
On the other hand, to establish the degree of approximation between the analytical model “MA” (the Laplace equation) and the numerical model “MD” (finite difference method), a Taylor series expansion was carried out, up to the fifth term, of an arbitrary value “u(x,y)” of the scalar field, with which said approach arrives at the following result
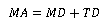
Where the term “TD” is called “discrepancy term” since it marked the quantitative difference between said mathematical models. Its analytical form obtained was the following
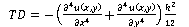
The term “h” represented the way the mesh had been sectioned. In addition to this, if the scalar field varied smoothly and the boundary conditions were homogeneous, a general solution to the Laplace differential equation could be obtained. In this solution, constants were generated that depended on the boundary
conditions, which revealed, for a specific stable physical system, the dependence of the TD on the square of h.
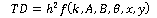
It clearly highlighted the fact that by making the term h smaller, this discrepancy term became irrelevant and consequently, both models, analytical and numerical, showed their approximation.
To solve the linear system of first degree equations, Cramer's rule was used. To create the algorithm, the Geogebra Classic software, Version 6.0.801.0, which is free, was used. The link to access this digital tool is the web address, https://www.geogebra.org/m/rmwrxxsa. The objective of the creation of this tool was based on the study of physical systems under equilibrium or stable conditions, such as: stable thermal flow over a conductive sheet, a static distribution of electrical potential on a surface, a pressure distribution that describes the stable flow of a fluid, etc.
Este obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional.
